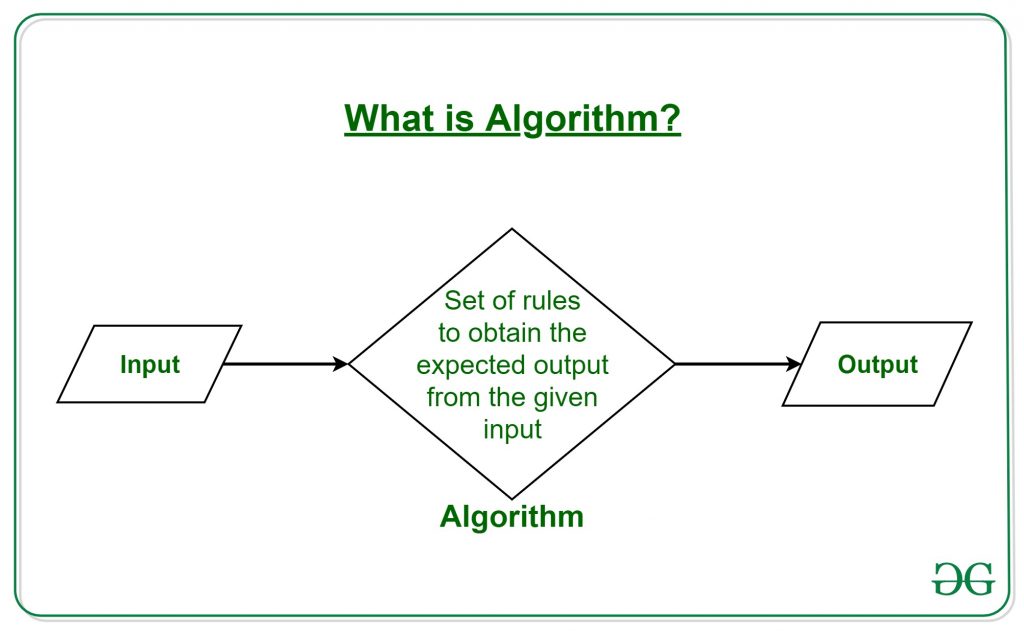
Apa Itu Algoritma?

ALGORITMA

        Kata Algoritma berarti “suatu proses atau seperangkat aturan yang harus diikuti dalam perhitungan atau operasi pemecahan masalah lainnya”. Oleh karena itu, Algoritma mengacu pada seperangkat aturan/instruksi yang selangkah demi selangkah menentukan bagaimana suatu pekerjaan akan dieksekusi untuk mendapatkan hasil yang diharapkan.

        Algoritma bisa dipahami dengan mengambil contoh memasak resep baru. Untuk memasak resep baru, seseorang membaca instruksi dan langkah-langkah dan menjalankannya satu per satu, dalam urutan yang diberikan. Hasil yang diperoleh adalah masakan baru yang dimasak dengan sempurna. Demikian pula, algoritma membantu melakukan tugas dalam pemrograman untuk mendapatkan output yang diharapkan.

        Karena sebagian orang tidak akan mengikuti instruksi tertulis untuk memasak resep, tetapi hanya beberapa yang standar. Demikian pula, tidak semua instruksi tertulis untuk pemrograman adalah algoritma. Agar beberapa instruksi menjadi suatu algoritma, ia harus memiliki karakteristik sebagai berikut :

• Clear and Unambiguous : Algoritma harus jelas dan tidak ambigu. Setiap langkahnya harus jelas dalam semua aspek dan harus mengarah pada satu makna saja.
• Well-Defined Inputs : Jika suatu algoritma mengatakan untuk mengambil input, itu harus menjadi input yang terdefinisi dengan baik.
• Well-Defined Outputs : Algoritma harus dengan jelas mendefinisikan output apa yang akan dihasilkan dan juga harus didefinisikan dengan baik.
• Finite-ness : Algoritma harus terbatas, yaitu tidak boleh berakhir dalam loop tak terbatas atau serupa.
• Feasible : Algoritma harus sederhana, generik dan praktis, sehingga dapat dieksekusi dengan sumber daya yang tersedia. Itu tidak boleh mengandung beberapa teknologi masa depan, atau apa pun.
• Language Independent : Algoritma yang dirancang harus bahasa-independen, yaitu harus hanya instruksi biasa yang dapat diimplementasikan dalam bahasa apapun, namun output akan sama, seperti yang diharapkan.

Keuntungan dari menggunakan algoritma :

• Hal ini mudah dimengerti.
• Algoritma adalah representasi langkah-bijaksana dari solusi untuk masalah yang diberikan.
• Dalam Algoritma, masalah dipecah menjadi bagian-bagian atau langkah-langkah yang lebih kecil sehingga lebih mudah bagi programmer untuk mengubahnya menjadi program yang sebenarnya.

Kelemahan dalam menggunakan algoritma :

• Penulisan algoritma membutuhkan waktu yang lama sehingga memakan waktu.
• Pernyataan Branching dan Looping sulit untuk ditampilkan dalam Algoritma.

Bagaimana cara mendesain sebuah algoritma?

Untuk menulis suatu algoritma, hal-hal berikut diperlukan sebagai ketentuan :

• Masalah yang harus diselesaikan dengan algoritma ini.
• Kendala masalah yang harus diperhatikan saat memecahkan masalah.
• Masukan yang akan diambil untuk memecahkan masalah.
• Output yang diharapkan ketika masalah tersebut terpecahkan.
• Solusi untuk masalah ini, dalam kendala yang diberikan.

Kemudian algoritma ditulis dengan bantuan parameter di atas sehingga menyelesaikan masalah.

Contoh :

Algoritma sederhana untuk menjumlahkan tiga bilangan dan mencetak totalnya.

Langkah 1: Memenuhi prasyarat / ketentuan

Seperti dibahas di atas, untuk menulis suatu algoritma, prasyaratnya harus dipenuhi.

1. Masalah yang harus diselesaikan dengan algoritma ini: Tambahkan 3 angka dan cetak jumlahnya.
2. Batasan masalah yang harus dipertimbangkan saat menyelesaikan masalah: Angka harus hanya berisi angka dan tidak boleh ada karakter lain.
3. Masukan yang akan diambil untuk memecahkan masalah: Tiga angka yang akan ditambahkan.
4. Output yang diharapkan ketika masalah terpecahkan: Jumlah dari tiga angka yang diambil sebagai input.
5. Solusi untuk masalah ini, dalam kendala yang diberikan: Solusinya terdiri dari menjumlahkan 3 angka. Ini dapat dilakukan dengan bantuan operator '+', atau sedikit bijaksana, atau metode lainnya.

Langkah 2: Merancang algoritma

Sekarang mari kita rancang algoritme dengan bantuan prasyarat di atas. Algoritma untuk menambahkan 3 angka dan mencetak jumlah mereka.

1. MULAI
2. Deklarasikan 3 variabel integer num1, num2 dan num3.
3. Ambil tiga angka, yang akan ditambahkan, sebagai input dalam variabel num1, num2, dan num3 masing-masing.
4. Mendeklarasikan jumlah variabel integer untuk menyimpan jumlah yang dihasilkan dari 3 angka.
5. Tambahkan 3 angka dan simpan hasilnya dalam jumlah variabel.
6. Cetak nilai jumlah variabel
7. AKHIR

Langkah 3: Menguji algoritma dengan mengimplementasikannya.

Untuk menguji algoritma, mari kita implementasikan dalam bahasa C++.

// Program C++ untuk menjumlahkan 3 bilangan

// dengan bantuan algoritma di atas

#include <bits/stdc++.h>

using namespace std;

  

int main()

{

     

    // Variabel untuk mengambil input 3 bilangan

    int num1, num2, num3;

  

    // Variabel untuk menyimpan jumlah yang dihasilkan

    int sum;

  

    // Mengambil 3 angka untuk diinputkan

    cout << "Enter the 1st number: ";

    cin >> num1;

    cout << " " << num1 << endl;

  

    cout << "Enter the 2nd number: ";

    cin >> num2;

    cout << " " << num2 << endl;

  

    cout << "Enter the 3rd number: ";

    cin >> num3;

    cout << " " << num3;

  

    // Kalkulasi jumlahnya menggunakan operasi +

    // dan simpan di variabel sum

    sum = num1 + num2 + num3;

  

    // Mencetak total 

    cout << "\nSum of the 3 numbers is: "

         << sum;

  

    return 0;

}

Output :

Enter the 1st number: 7

Enter the 2nd number: 5

Enter the 3rd number: 3

Sum of the 3 numbers is: 13

Analisis teoritis dari sebuah algoritma :

1. Priori Analysis : “Priori” berarti “sebelum”. Oleh karena itu analisis Priori berarti memeriksa algoritma sebelum implementasinya. Dalam hal ini, algoritma diperiksa ketika ditulis dalam bentuk langkah-langkah teoritis. Efisiensi suatu algoritma diukur dengan mengasumsikan bahwa semua faktor lain, misalnya, kecepatan prosesor, adalah konstan dan tidak berpengaruh pada implementasi. Ini biasanya dilakukan oleh perancang algoritma. Dalam metode ini, Kompleksitas Algoritma ditentukan.

2. Posterior Analysis : “Posterior” berarti “setelah”. Oleh karena itu analisis Posterior berarti memeriksa algoritma setelah implementasinya. Dalam hal ini, algoritma diperiksa dengan mengimplementasikannya dalam bahasa pemrograman apa pun dan mengeksekusinya. Analisis ini membantu untuk mendapatkan laporan analisis aktual dan nyata tentang kebenaran, ruang yang dibutuhkan, waktu yang dikonsumsi, dll.

• Time Factor : Waktu diukur dengan menghitung jumlah operasi kunci seperti perbandingan dalam algoritma pengurutan.
• Space Factor : Ruang diukur dengan menghitung ruang memori maksimum yang dibutuhkan oleh algoritma.

- Space Complexity : Kompleksitas ruang dari suatu algoritma mengacu pada jumlah memori yang dibutuhkan algoritma ini untuk mengeksekusi dan mendapatkan hasilnya. Ini bisa untuk input, operasi sementara, atau output. 

Bagaimana cara menghitung Kompleksitas Ruang?

Kompleksitas ruang dari suatu algoritma dihitung dengan menentukan 2 komponen berikut:

• Fixed Part : Ini mengacu pada ruang yang pasti dibutuhkan oleh algoritma. Misalnya, variabel input, variabel output, ukuran program, dll.
• Variable Part : Ini mengacu pada ruang yang dapat berbeda berdasarkan implementasi algoritma. Misalnya, variabel sementara, alokasi memori dinamis, ruang tumpukan rekursi, dll.

- Time Complexity : Kompleksitas waktu dari suatu algoritma mengacu pada jumlah waktu yang dibutuhkan algoritma ini untuk mengeksekusi dan mendapatkan hasilnya. Ini bisa untuk operasi normal, pernyataan if-else bersyarat, pernyataan loop, dll.

Bagaimana cara menghitung Kompleksitas Waktu?

Kompleksitas waktu suatu algoritma juga dihitung dengan menentukan 2 komponen berikut:

• Constant Time Part : Setiap instruksi yang dieksekusi hanya sekali datang di bagian ini. Misalnya input, output, if-else, switch, dll.
• Variable Time Part : Setiap instruksi yang dieksekusi lebih dari sekali, katakanlah n kali, datang di bagian ini. Misalnya, loop, rekursi, dll.